Living on Curves

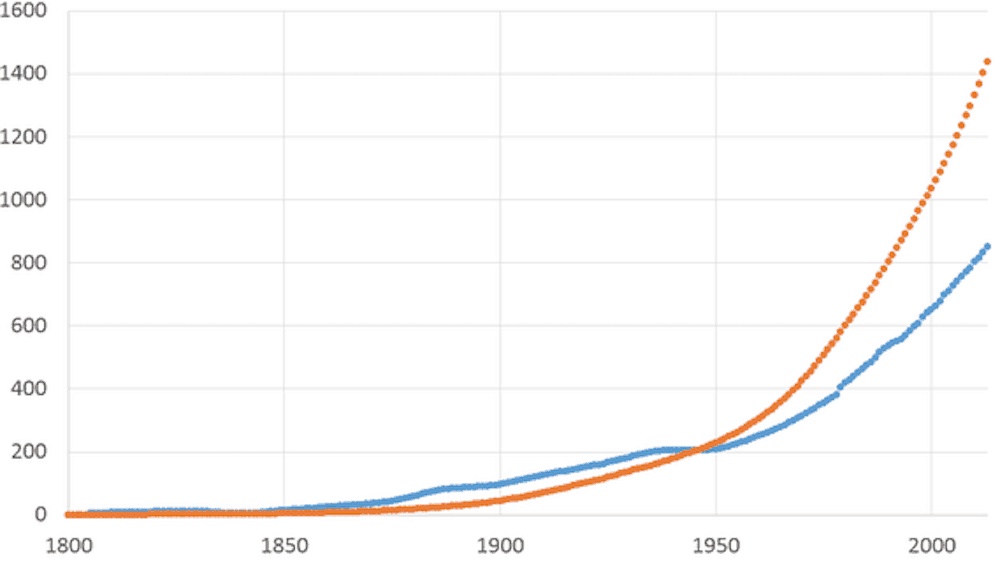
As of April 9, more than 15,000 people had died from COVID-19 in the US. That’s a quarter of the number of people that died from the flu during the 2017-18 season. It’s a fraction of the number of gun deaths, traffic fatalities, and suicides each year. It’s a small fraction of the 600,000 cancer deaths each year in the US.

Given the relative risks, it’s interesting that the US economy has been put in a medically induced coma throwing tens of millions out of work for what appears to be a small risk.

The difference is the curve. It’s the latency of the disease (the two asymptomatic weeks you run around infecting people) and the exponential rate of infection that is scary. The US death toll may be 60,000 to 80,000 by August.

The weird thing about this pandemic is being told to take precautions when it doesn’t appear warranted by local circumstances. It runs counter to our “gut feeling” about what we should do. We’re just not very good at living on a curve and thinking mathematically.

We’ve been here before. This is all a compressed version of living on the exponential technology curve. Gordon Moore predicted 50 years ago that we could expect the speed and capability of our computers to increase every couple of years, and we will pay less for them. Moore’s law has driven exponential change in computing power.

Almost 20 years ago Ray Kurzweil explained, “ When people think of a future period, they intuitively assume that the current rate of progress will continue for future periods. However, careful consideration of the pace of technology shows that the rate of progress is not constant, but it is human nature to adapt to the changing pace, so the intuitive view is that the pace will continue at the current rate. Even for those of us who have been around long enough to experience how the pace increases over time, our unexamined intuition nonetheless provides the impression that progress changes at the rate that we have experienced recently.”

The rise of machine learning, driven by faster chips and data from a world full of mobile devices, has extended Moore’s prediction by making fast machines smarter.

For many, it was Tim Urban’s post in 2015 on artificial intelligence where he made the case that “In order to think about the future correctly, you need to imagine things moving at a much faster rate than they’re moving now.”

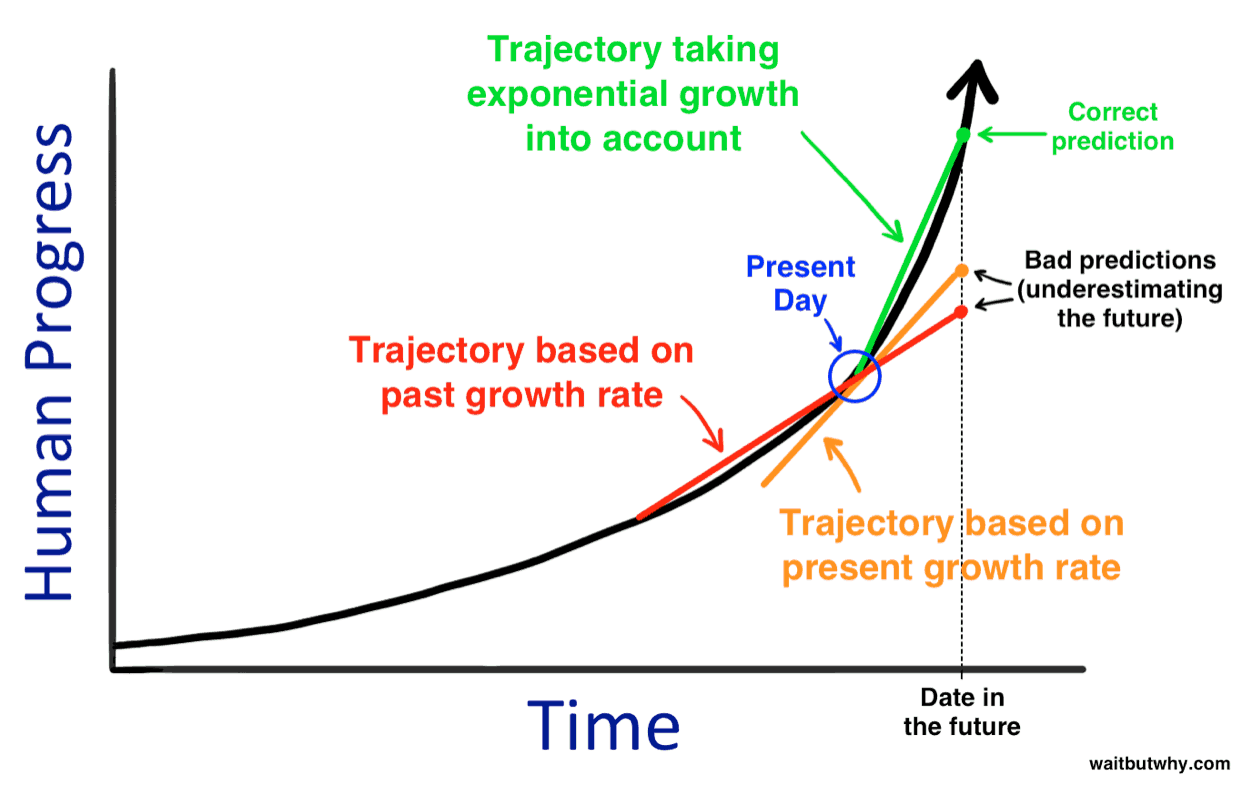
Urban illustrated our tendency to predict the future based on a linear view of the past when technologic capabilities are increasing exponentially.

Add climate change to the mix of life-altering curves that have not produced a relevant response. Human-caused emissions of carbon dioxide were pretty linear until the middle of the last century when they became exponential resulting in accelerating warming of the planet (see featured image where the orange line is human emissions, the blue line is atmospheric CO2). But again, it’s life on a curve–our behavior today will impact life on the planet decades from now.

Our kids are growing up on a curve–a public health curve, an exponential technology curve, and a climate curve. These curves demand personal and collective behavior change but the outcome distributions behind these curves either don’t register or move us to action. Almost all of us maintain a normality bias where we assume things will go on about the same as they always have.

How do we build a data science mindset–a curiosity about the data behind the headlines?

How do we reflect on whether a change in conditions is linear or exponential? And, how do we turn that realization into action? These are all questions we should be asking ourselves as adults. Right now, with a billion children at home, it’s a good time to help them think about living on a curve.

There are some great online resources to kickstart the curve conversation. One author suggests clearing out the living room and plotting the curve on the floor to make it visceral. If that seems excessive, check out the 3Blue1Brown video that walks through the math of pandemic. This PBS video explains the paradox of pandemic.

Frank Wang, President of the Oklahoma School of Science and Math, has some great resources on Facebook. “What’s unfolding is a catastrophe, but it’s also a time to share rich math and teach about the concepts of calculus—the mathematics of change. For young people, it can be a way to motivate their learning of mathematics,” says Wang. “Where teaching about exponential growth might have them scratching their heads in the classroom, now we can show that these models are being used in hospitals to calculate things like: how many ventilators, or how many hospital beds, will they need?”

This is a great time to invite young people into a conversation about complex systems. “Understanding and applying the concepts of complex adaptive systems may not prevent the next virus outbreak. But if we fail to use them, we will be ensuring the next pandemic.,” said Ambassador (Ret.) David Carden.

Young people are growing up on a jostling set of curves that will bring waves of dislocations to their lives. And even though we don’t fully understand the questions, much less the answers, it’s a good time to start this conversation with our children.